


Balancing Redox Equations may seem complex to other people. But you will be surprised to know that there is another way around to do this! I will now teach you the steps on how to balance these equations the easy way.
The Half-Reaction Method, also called the ion-electron method, is an alternative method of balancing redox equations. Although it is easier in some way, it is only limited to reactions taking place in water solution in which electrons are completely lost or gained by the reactants. The basic principle behind this method is similar to the basis of balancing redox equations using oxidation numbers.

STEPS IN USING THE HALF REACTION METHOD
(With Acids)
SAMPLE PROBLEM:
In a water solution with an acid pH, the nitrate ion, NO3- will react with iodine, I2, to provide the iodate ion, IO3-, and nitrogen dioxide, NO2.
Balance the equation.
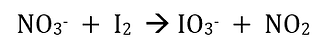
Step 1. Divide the equation into its two half reaction equations, and, using oxidation numbers, identify which half reaction is oxidation and what is reduction.
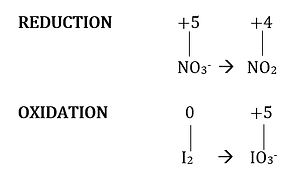
Step 2. Balance the half-reaction equation for the reduction. Nitrogen is already balanced so the only problem is how to balance the oxygen. By adding one H2O molecule to the right, oxygen can be balanced. Because of this, there will be an added H2 molecule on the right side, so you’ll also put 2H+ on the left side to balance.
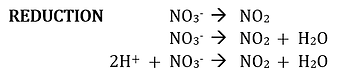
The equation now is balanced with respect to H, N, and O atoms, but it is not completely balance because of unequal charge. The molecules on the left give the left side a net charge of 1+, whereas the neutral molecules on the right gives a net charge of 0. To give the left side a net charge of 0, add one electron e- to the left side:
Step 3. Use the same procedure in Step 2 to balance the half-reaction equation for oxidation.
Balance the number of I atoms by providing a coefficient of 2 for the IO3- ion. Balance the number of O atoms by adding six H2O molecules to the left. Finally, balance the number of H atoms by adding 12 H+ ions to the right.

Step 4. Multiply each term in one of the of the half-reaction equations by a factor that will make the number of electrons in the oxidation equal to the number gained in the reduction.
Note that in the reduction, 1 electron is gained, but that in the oxidation, 10 electrons are lost. The gain can be made equal to the loss by multiplying each term in the reduction equation by 10.
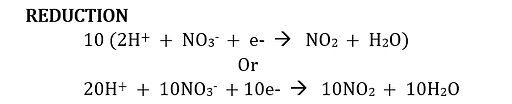
Step 5. Referring to the two half-reaction equations in which the number of electrons lost equals the number gained, add the two half-reaction equations to get the overall equation.
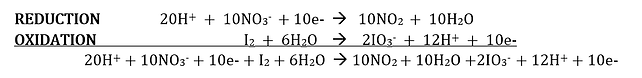
Step 4. Simplify the overall equation by collecting similar terms. The 10e- on each side of the equation ban be subtracted out. The 20H+ on the left and the 12H+ on the right give a net amount of 8H+ on the left. The 6H2O on the left and the 10H2O on the right give a net amount of 4H2O on the right. The equation is thus simplified as:

As a final check on the equation, we can see that the oxygen balances. A count of the oxygen atoms shows that there are 30 oxygen atoms on each side.
Other redox reactions take place in water solutions with a basic pH.
1. Do the half reaction method as if it is in acidic solution. Then, convert all H+ to H2O.
2. The number of H2O will determine the number of OH- (hydroxide ions) you should add on the other side.
3. Do the next processes according to the Half-Reaction method of Balancing Redox Reactions.
In these basic solutions, hydroxide ions, OH-, and water molecules, H2O may be reactants or products. Therefore, in redox reactions that take place in basic solution, H2O and OH- can be added to the half-reaction equations as needed to make the number of oxygen and hydrogen atoms balanced.
STEPS IN USING THE HALF REACTION METHOD
(With Bases)
References:
-
Prentice Hall Chemistry : The Study of Matter
-
Sir Jeff's discussion and Chemistry notes
-
Google.com

